Video: Cos'è la regressione lineare regolarizzata?
2024 Autore: Lynn Donovan | [email protected]. Ultima modifica: 2023-12-15 23:49
regolarizzazione . Questa è una forma di regressione , che vincola/regolarizza o riduce le stime dei coefficienti verso lo zero. In altre parole, questa tecnica scoraggia l'apprendimento di un modo più complesso o flessibile modello , in modo da evitare il rischio di sovradattamento. Una semplice relazione per regressione lineare Somiglia a questo.
Di conseguenza, cos'è lambda nella regressione lineare?
Quando abbiamo un alto grado lineare polinomio che viene utilizzato per adattare un insieme di punti in a regressione lineare setup, per prevenire il sovradattamento, usiamo la regolarizzazione e includiamo a lambda parametro nella funzione di costo. Questo lambda viene quindi utilizzato per aggiornare i parametri theta nell'algoritmo di discesa del gradiente.
In secondo luogo, qual è lo scopo della regolarizzazione? regolarizzazione è una tecnica usata per accordare il funzione aggiungendo un termine di penalità aggiuntivo nell'errore funzione . Il termine aggiuntivo controlla l'eccessiva fluttuazione funzione tale che i coefficienti non assumano valori estremi.
In questo modo, perché abbiamo bisogno di regolarizzare in regressione?
L'obiettivo di regolarizzazione è evitare il sovradattamento, in altre parole noi stanno cercando di evitare modelli che si adattano molto bene ai dati di addestramento (dati usati per costruire il modello), ma si adattano male ai dati di test (dati usati per testare quanto è buono il modello). Questo è noto come overfitting.
Cosa significa regolarizzazione?
In matematica, statistica e informatica, in particolare nell'apprendimento automatico e nei problemi inversi, la regolarizzazione è il processo di aggiunta di informazioni per risolvere un problema mal posto o per prevenire il sovradattamento. regolarizzazione si applica alle funzioni obiettivo in problemi di ottimizzazione mal posti.
Consigliato:
Cos'è lineare e non lineare nella struttura dei dati?
1. In una struttura dati lineare, gli elementi dati sono disposti in un ordine lineare in cui ogni elemento è collegato al suo precedente e successivo adiacente. In una struttura di dati non lineare, gli elementi di dati sono collegati in modo gerarchico. Nella struttura dati lineare, gli elementi dati possono essere attraversati solo in una singola corsa
Che cos'è la regressione ML?
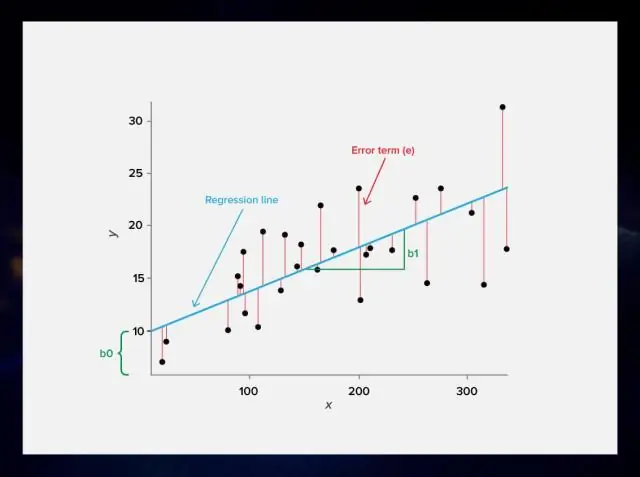
La regressione è un algoritmo ML che può essere addestrato per prevedere output numerati reali; come temperatura, prezzo delle azioni, ecc. La regressione si basa su un'ipotesi che può essere lineare, quadratica, polinomiale, non lineare, ecc. L'ipotesi è una funzione che si basa su alcuni parametri nascosti e sui valori di input
Che cos'è il metodo dell'albero di regressione?
La metodologia di costruzione dell'albero di regressione generale consente alle variabili di input di essere una combinazione di variabili continue e categoriali. Un albero di regressione può essere considerato come una variante degli alberi decisionali, progettato per approssimare funzioni a valori reali, invece di essere utilizzato per metodi di classificazione
Che cos'è un problema di regressione nell'apprendimento automatico?
Un problema di regressione si verifica quando la variabile di output è un valore reale o continuo, come "stipendio" o "peso". Possono essere utilizzati molti modelli diversi, il più semplice è la regressione lineare. Cerca di adattare i dati con il miglior iperpiano che passa attraverso i punti
Che cos'è l'analisi dell'albero di regressione?
L'analisi dell'albero di regressione è quando il risultato previsto può essere considerato un numero reale (ad esempio il prezzo di una casa o la durata della degenza di un paziente in ospedale)