Sommario:
Video: Dove viene utilizzato l'ordinamento di unione?
2024 Autore: Lynn Donovan | [email protected]. Ultima modifica: 2023-12-15 23:49
Unisci ordinamento : Usato negli scenari di database, perché stabile (multi-chiave ordinare ) ed esterno (i risultati non rientrano tutti nella memoria). Utile in scenari distribuiti in cui arrivano dati aggiuntivi durante o dopo ordinamento . Il consumo di memoria impedisce un uso più ampio su dispositivi di piccole dimensioni, ma esiste la versione Nlog^2N sul posto.
Tenendo presente questo, dove viene utilizzato l'ordinamento per inserzione?
Usi: Ordinamento inserimento è Usato quando il numero di elementi è piccolo. Può anche essere utile quando l'array di input è quasi smistato , solo pochi elementi sono fuori posto in un grande array completo. Cos'è il binario? Ordinamento inserimento ? Possiamo usare la ricerca binaria per ridurre il numero di confronti nella normalità ordinamento di inserimento.
Inoltre, sai, cos'è l'ordinamento di unione con l'esempio? Un esempio di unisci ordinamento . Prima dividi l'elenco nell'unità più piccola (1 elemento), quindi confronta ogni elemento con l'elenco adiacente a ordinare e unire le due liste adiacenti. Finalmente tutti gli elementi sono smistato e unito . Unisci ordinamento è un algoritmo divide et impera inventato da John von Neumann nel 1945.
Rispetto a questo, perché viene utilizzato il merge sort?
Unisci ordinamento è utile per ordinamento elenchi collegati. Unisci ordinamento è una stalla ordinare il che significa che lo stesso elemento in un array mantiene le loro posizioni originali l'uno rispetto all'altro. Complessità temporale complessiva di Unisci ordinamento è O(nLogn). È più efficiente in quanto nel peggiore dei casi anche il runtime è O(nlogn)
Come si usa il merge sort?
Ecco come il merge sort utilizza il divide et impera:
- Dividi trovando il numero q della posizione a metà strada tra p ed r.
- Conquista ordinando ricorsivamente i sottoarray in ciascuno dei due sottoproblemi creati dal passaggio di divisione.
- Combina unendo i due sottoarray ordinati nuovamente nel singolo sottoarray ordinato [p..
Consigliato:
Dove viene utilizzato un interruttore a pulsante?
Gli interruttori a pulsante sono utilizzati in tutte le applicazioni industriali e mediche e sono riconoscibili anche nella vita di tutti i giorni. Per usi nel settore industriale, i pulsanti sono spesso parte di un sistema più grande e sono collegati tramite un collegamento meccanico
L'unione esterna è uguale all'unione esterna completa?
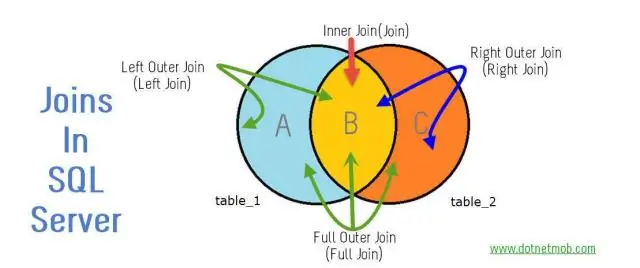
Nei join esterni, tutti i dati correlati di entrambe le tabelle vengono combinati correttamente, più tutte le righe rimanenti di una tabella. In full outer join, tutti i dati vengono combinati ove possibile
Dove viene utilizzato Redux?
Redux viene utilizzato principalmente per la gestione dello stato dell'applicazione. Per riassumere, Redux mantiene lo stato di un'intera applicazione in un singolo albero di stato immutabile (oggetto), che non può essere modificato direttamente. Quando qualcosa cambia, viene creato un nuovo oggetto (usando azioni e riduttori)
Dove viene utilizzato il groove?
Lingua madre: Java
Dove viene utilizzato il p2p?
Come accennato in precedenza, il P2P viene utilizzato per condividere tutti i tipi di risorse di elaborazione come potenza di elaborazione, larghezza di banda di rete o spazio di archiviazione su disco. Tuttavia, il caso d'uso più comune per le reti peer-to-peer è la condivisione di file su Internet