Video: Le diagonali di un angolo quadrato sono bisettrici?
2024 Autore: Lynn Donovan | [email protected]. Ultima modifica: 2023-12-15 23:49
Il quadrato ha le seguenti proprietà:
Si applicano tutte le proprietà di un rombo (quelle che contano qui sono i lati paralleli, diagonali sono bisettrici perpendicolari l'uno dell'altro, e diagonali bisecare il angoli ). Si applicano tutte le proprietà di un rettangolo (l'unica che conta qui è diagonali sono congruenti).
Quindi, le diagonali di un rettangolo sono bisettrici?
Il diagonali di un rettangolo dividerà in due solo il angoli se i lati che si incontrano al angolo sono uguali: in altre parole, solo se i rettangolo è un quadrato. Un altro modo di pensarla: il angolo è un diritto- angolo , e il bisettrice dell'angolo deve uscire a metà a destra- angolo ai lati. Quindi il rettangolo deve essere quadrato.
Ci si potrebbe anche chiedere, la diagonale del quadrato è bisettrice? UN quadrato è un caso speciale di trapezio isoscele, aquilone, parallelogramma, quadrilatero, rettangolo, rombo e trapezio. Il diagonali di una bisettrice quadrata uno un altro e sono perpendicolari (illustrati in rosso nella figura sopra). Inoltre, loro dividere in due coppia di angoli opposti (illustrati in blu).
Considerato questo, in quali quadrilateri le diagonali bisecano gli angoli?
UN quadrilatero è un rombo se: è un parallelogramma e una coppia di lati adiacenti sono uguale, è diagonali bisettrici l'un l'altro a destra angoli , suo diagonali bisettrici ogni vertice angolo.
Qual è la diagonale del quadrato?
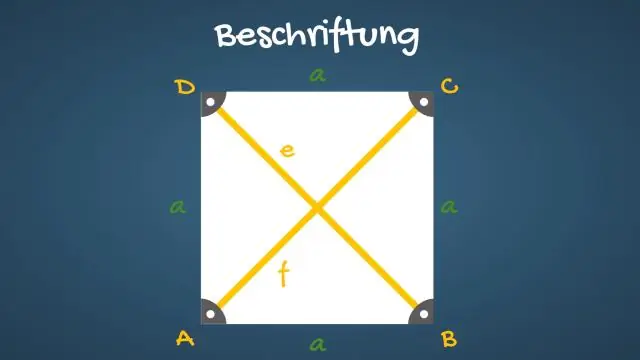
diagonali di una quadrato . UN quadrato ha due diagonali , che sono segmenti di linea che collegano i vertici opposti (angoli) del quadrato . In altre parole, il punto in cui diagonali interseca (croce), divide ciascuno diagonale in due parti uguali. Ogni diagonale divide il quadrato in due triangoli rettangoli isosceli congruenti.
Consigliato:
Cosa sono le icone con una piccola freccia nell'angolo in basso a sinistra?
La piccola freccia nell'angolo in basso a sinistra di un'icona indica che l'icona è un'icona di collegamento. Le icone di collegamento servono per avviare il programma che rappresenta
Le diagonali del quadrato sono uguali?
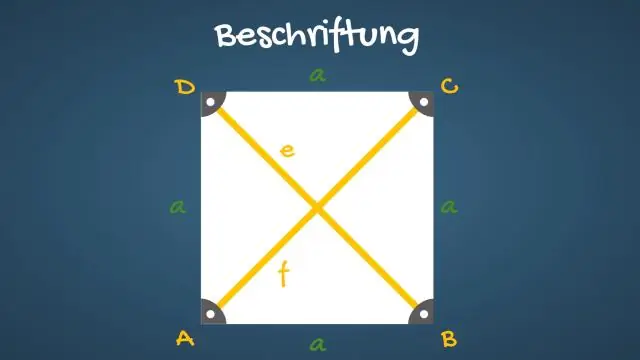
Le diagonali di un quadrato bisecano i suoi angoli. I lati opposti di un quadrato sono paralleli e di uguale lunghezza. Tutti e quattro i lati di un quadrato sono uguali. Le diagonali di un quadrato sono uguali
Le due diagonali di un parallelogramma sono uguali?
Quando un parallelogramma è diviso in due triangoli, vediamo che gli angoli attraverso il lato comune (qui la diagonale) sono uguali. Questo dimostra che anche gli angoli opposti in un parallelogramma sono uguali. Le diagonali di un parallelogramma non sono di uguale lunghezza
Un quadrato ha una simmetria di mezzo giro?
Un quadrato è più simmetrico della lettera O, ma meno simmetrico del cerchio. Se giri un quadrato di 90°, sembrerà esattamente come era all'inizio, ma se lo giri di un angolo inferiore a 90°, non sembrerà lo stesso. Un quadrato ha una simmetria rotazionale di 1/4 di giro (o simmetria rotazionale di 90°)
Come si rimuove un tappo a tubo quadrato?
Se deve essere rimosso un tappo a testa quadrata, battere sulla testa del tappo usando un martello da una libbra. I colpi ritmici, non troppo forti, dovrebbero essere usati e continuati per un minuto o più. Un penetrante spray, come WD-40, aiuta sempre. Utilizzare una chiave grande, come una mezzaluna da 12 pollici per rimuovere la spina